Ya casi es una tradición, en la Facultad de Ciencias de la UNAM, que los profesores o sus asistentes organicen chanzas a manera de novatada para los alumnos de nuevo ingreso. Quizá la más engañosa e ingeniosa sea aquella que involucra dos objetos matemáticos, que como el epíteto sugiere, residen principalmente en el intelecto, y que además un alumno de primer semestre difícilmente reconocería.
La novatada consiste en solicitar que los alumnos compren una máquina de Turing o una botella de Klein como requisito para el primer examen, no obstante que el nombre de la primera insinúa el de una popular marca de chocolates o de algún sistema para mejorar el desempeño de un automóvil, mientras que la segunda parece referirse a un conocido perfume de diseñador; ambos objetos son intangibles por naturaleza.
La máquina

La máquina de Turing —mt, en adelante— recibe el nombre de su creador, el matemático inglés Alan M. Turing (1912-1954) considerado por muchos como el padre de la informática moderna, y quien además tuvo un rol fundamental en el desciframiento del código de las máquinas Enigma, mediante el cual las fuerzas navales de la Alemania nazi enviaban y recibían mensajes cifrados, es decir, ininteligibles para cualquier profano que tuviera acceso al mensaje.1
Por dicha labor, podría decirse que Alan Turing fue también pionero en el estudio matemático de la criptografía, o como actualmente se le conoce: criptoanálisis
.
Corría la década de 1930, y algunos miembros de la comunidad matemática aún dirigían sus esfuerzos sobre varios de los problemas propuestos por el matemático alemán David Hilbert en los albores del siglo XX. Algunos de los 23 problemas propuestos por Hilbert resultaron ser muy influyentes en cómo se desarrollaría la matemática, y su filosofía, a lo largo del siglo pasado.
Pues bien, el mundo aún no se recuperaba del golpe asestado por el matemático alemán Kurt Gödel al resolver el segundo problema de Hilbert —golpe que tuvo enormes repercusiones sobre la filosofía de la matemática y sobre la propia ciencia— cuando Alan Turing sintió que el trabajo de Gödel aún dejaba pendiente la pregunta sobre la existencia de un mecanismo, que al menos en principio, decida si una proposición matemática es verdadera o falsa —piense el lector en un oráculo al cual preguntamos si es cierto o falso que cualquier entero par y mayor a 2 puede escribirse como la suma dos números primos.
Esa pregunta, acerca de la existencia de dicho mecanismo, es lo que se conoce en el mundo de las matemáticas como el Entscheidungsproblem —‘Problema de la Decisión’, en alemán— y sobrevivió al embate de Gödel, pues resolverlo requería una definición formal de la noción de mecanismo; y fue precisamente esto lo que Turing logró al concebir su máquina.

Lo novedoso del acercamiento de Turing fue la reformulación de la pregunta de Hilbert en términos de computación de números, y no en términos de demostraciones.
Así, Turing comienza su trabajo preguntándose: ¿Cómo podemos especificar lo infinito en términos finitos?; por ejemplo: ¿cómo podemos especificar finitamente la secuencia infinita de los dígitos de π, ese loco número irracional? El día de hoy, cualquier persona que sepa emplear un lenguaje de programación de computadoras podrá dar una respuesta a la pregunta anterior, pero para eso Turing tuvo que definir y delimitar el concepto de algoritmo, es decir, el conjunto de pasos que se deben realizar para resolver algún problema; y ésta es precisamente la esencia de la mt.
La botella de Klein
Este objeto recibe su nombre a partir de otro matemático alemán llamado Felix Klein (1849- 1925). El paradigma revolucionario de este científico consistió en visualizar la geometría como el estudio de las propiedades de un espacio que permanece invariante bajo un grupo de transformaciones –por ejemplo, la noción de simetría de una figura dibujada sobre una hoja de papel puede expresarse diciendo que la figura permanece invariante bajo una reflexión o una traslación, aunque no siempre es así.
Felix Klein propuso una novedosa e influyente manera de concebir la geometría. Con dicha propuesta ya se sugiere el estudio de otra rama muy importante de las matemáticas: la topología, y es en ella donde Klein nos ofrece el objeto por el cual le recordamos aquí.La rama de las matemáticas llamada «topología», está interesada en todo aquello que se puede obtener estirando y pegando cosas.
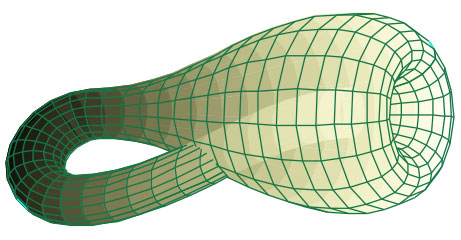
La bk posee algunas curiosidades, amén de haber sido bautizada tras un error de traducción2 Originalmente, este objeto era conocido como «superficie de Klein», mas un error en la traducción hizo que se le conociera posteriormente como «botella de Klein».; primero, esta botella posee un solo lado –es decir, no se pueden distinguir interior y exterior–, y es no-orientable –al recorrer su extensión, la siguiente vez que pisemos el punto de partida, estaremos de cabeza. Esta botella no posee borde, sino que en este aspecto se parece mucho a una esfera, la cual podemos recorrer en toda su extensión sin temor a caer al vacío o al limbo donde habita el geómetra Euclides.
A pesar de que es claro por qué es imposible adquirir cualquiera de los objetos que hemos descrito, algunos alumnos, motivados por sus taimados profesores, se han aventurado a preguntar en cualquier tienda por la disponibilidad de alguno de ellos.
Para que conozcas mejor el pensamiento matemático de Turing y la botella de Klein consulta este artículo completo en Algarabía 134.
También te interesará:















