¿Cuántas horas hemos visto pasar esperando nuestro turno en alguna sucursal bancaria, en las atestadas cajas de un supermercado o en la pedestre cola de las tortillas? Estos ejemplos de filas sirven para estudiar la teoría que sentó las bases de las telecomunicaciones actuales y su relación con nuestras actividades cotidianas.
La historia de la teoría de colas coincide con el quehacer de un destacado matemático e ingeniero danés, Agner Krarup Erlang (1878-1929), quien durante 20 años ayudó a la Copenhagen Telephone Company —ctc—, entonces subsidiaria de la compañía telefónica Bell, a resolver problemas avanzados de comunicaciones.

Uno de los problemas fundamentales era calcular cuántos circuitos telefónicos —también llamados troncales—1 Se llama «troncales de conexión interurbana» a las líneas salientes que conectan a uno o más centros de conmutación cercanos, en contraste con las líneas individuales que conectan a cada teléfono con la oficina central más cercana. [Andrew S. Tanembaum, Redes de computadoras; México: Pearson, 2003.] eran necesarios para que los habitantes de dos poblados se comunicaran.
Los problemas técnicos de los circuitos telefónicos involucran el concepto del azar en matemáticas y, por tanto, la noción de probabilidad, que es la rama de las matemáticas que se ocupa de estudiar los fenómenos aleatorios y encuentra soluciones para medirlos. ¿En cuánto podía estimarse la duración de cada llamada, cuántas llamadas se realizarían y en qué momento se esperarían los picos con el mayor número de éstas?
La búsqueda del mejor servicio
Si usted está leyendo esto mientras hace la cola de las tortillas —o cualquier otra—, seguramente se preguntará: ¿cuánto falta para que me atiendan?, y también, ¿qué tiene que ver la telefonía con la teoría de colas? En una red telefónica y en una cola —o sistema de colas—, el papel del azar es crucial, en esta última, desde los tiempos hasta el número de personas o elementos en espera de ser «atendidos». ¿Cómo lograr que el sistema sea eficiente?

En el estudio de un sistema de colas nos encontramos con procesos y eventos1 En probabilidad, un evento es un subconjunto del espacio muestral, e involucra a algunos de entre todos los posibles resultados de un experimento aleatorio llevado a cabo en ese espacio. que evolucionan de forma aleatoria
en el tiempo; es decir, cuyo comportamiento no podemos predecir con absoluta certeza. Por esta razón, se utilizan modelos matemáticos que permiten analizar y predecir el comportamiento estocástico 2 Relativo al azar. La teoría estocástica es la «teoría estadística de los procesos cuya evolución en el tiempo es aleatoria, tal como la secuencia de las tiradas de un dado», según el drae. de las colas —o el papel del azar en éstas—. Tomemos, por ejemplo, lo que sucede en un sistema de colas con el que nos llevamos muy bien o muy mal, dependiendo, en gran medida, de nuestro estado de ánimo: las filas del supermercado.
El estudio de las colas
Basándonos en el ejemplo del súper, un sistema de colas es aquél en donde los «clientes» llegan a una «unidad de servicio» —en este caso, el área de cajas— de acuerdo con un «proceso de llegada».
La «unidad de servicio» puede tener uno o más «servidores» —cajas y cajeros—. En el modelo más simple, se da por descontado que un servidor puede atender sólo a un cliente
a la vez —como en el súper—. Esto implica que si un
cliente encuentra ocupados todos los servidores, deberá forzosamente hacer cola. Al final, el cliente recibirá el servicio y procederá a retirarse del sistema.
A fin de explicar el funcionamiento de una cola, es necesario describirla analíticamente, formular un modelo matemático y encontrar los parámetros que la caracterizan.

Comencemos pues por describir los tres componentes principales del sistema de colas:
El proceso de entrada. Se consideran tres aspectos:
el tamaño de la población de llegada —¿cuántos?—, los diversos patrones de llegada —¿cómo?— y el comportamiento de los clientes —por ejemplo, ¿cuánto tiempo están «dispuestos» a esperar?
La estructura del sistema. Se analizan, en principio, dos aspectos: el número y modo en que los servidores se distribuyen, y la capacidad del sistema.
El proceso de salida. Trata de cómo se selecciona a los clientes que recibirán el servicio y en qué orden se les otorgará. Los principales criterios son:
– First Come First Served (fcfs) —El primero que llega es el primero que recibe el servicio—. Ejemplos de éste son: los cajeros del supermercado, el banco, el cine, la cola de las tortillas y muchísimos más.
– Last Come First Served (lcfs) —El último que llega es el primero que recibe el servicio—. Un ejemplo es cuando se apilan papeles sobre la mesa; si una persona llega, seguramente comenzará a ver el último que se dejó, es decir, el que está más arriba, e irá bajando hasta llegar al primero con el que se comenzó la pila.
Por supuesto, los términos genéricos para describir las partes de un sistema de colas serán sustituidos por los nombres que cada elemento recibe en la práctica, de acuerdo con el área de aplicación, tal como lo hicimos en nuestro ejemplo del supermercado. Ahora bien, hablemos del carácter revolucionario de esta teoría.
«Durante el siglo xx el avance tecnológico más importante fue la obtención, el procesamiento y la distribución de la información», Andrew W. Tanenbaum.
Su aplicación en las telecomunicaciones
De acuerdo con el profesor estadounidense Andrew S. Tanenbaum, «durante el siglo xx el avance tecnológico más importante fue la obtención, el procesamiento y la distribución de la información. Entre otros acontecimientos, vimos la instalación de redes mundiales de telefonía, la invención de la radio y la televisión, el nacimiento sin precedentes de la industria de la computación, así como el lanzamiento
de satélites de comunicaciones».
En el mundo actual, si se trata de una computadora, podemos hablar de tareas que hacen cola en el cpu o dispositivos de entrada o salida en diferentes etapas del sistema de colas. Si, por otro lado, hablamos de las redes de datos, nos referimos a paquetes con información que viajan a través de Internet y que hacen cola en los switches, hubs, routers y demás elementos, en espera de ser transmitidos.
La historia de la teoría de colas está íntimamente relacionada con el análisis de procesos que ocurren de forma aleatoria; su origen está en las primeras predicciones a propósito de los juegos de azar.
Sirva de ejemplo lo que sucede cuando uno enciende su computadora y ésta se conecta a la red. Por el cable de cuatro pares de hilos llamado coloquialmente «de red» 3 Técnicamente, se llama «cable Ethernet», por el tipo de tecnología que utiliza para transmitir la señal. —si la conexión es física—, la información circula en la forma de «paquetes de datos» que contienen, entre otros parámetros, la dirección de Internet a la que deberán entregarse.
Sin embargo, puesto que éstos son enviados a gran velocidad, los paquetes hacen cola como si fueran pequeños clientes
de un banco en espera de ser despachados, tanto al llegar a su destino como en los puntos intermedios o nodos —que en su mayoría serán routers, encargados de redireccionar los paquetes de datos—, hasta que el router los envía al siguiente nodo o llegan a su destino.
Hoy las nuevas tecnologías están ampliamente diversificadas; lo que además ha puesto énfasis en la necesidad de compartir recursos —desde fuentes de energía hasta los servidores de gigantes de Internet como Google— con mayor eficiencia. Esto, aunado al aumento en el número de usuarios y dispositivos que comparten estos recursos, le ha dado un vuelco insospechado a las telecomunicaciones modernas. No obstante, en sus inicios, éstas no habrían podido existir sin la teoría de colas.
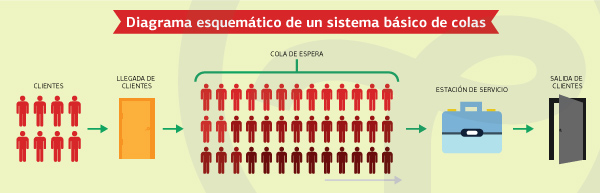
Te presentamos un diagrama de un sistema básico de colas.