Las sombras nos persiguen todo el tiempo. Han consternado a poetas, escritores, artistas, científicos y a personajes de ficción. Para algunos, las sombras representan deseos inconscientes; para otros, la sabia conjunción de éstas con la luz es lo que da equilibrio al alma y al lienzo; para algunos más, la sombra es una juguetona silueta que demanda el ejercicio de su libre albedrío y, finalmente, para unos cuantos, las sombras son elementos para medir al mundo, para conocer algo más de él.

Un ejemplo del último caso es el de Tales de Mileto (c a . 624-546 a.C.), filósofo y matemático originario de la actual Turquía, quien en uno de sus viajes al majestuoso Egipto sorprendió al faraón Amasis y a todo su séquito gracias a este designio de la oscuridad.
A pleno Sol
La leyenda cuenta que el gran sabio de Grecia fue desafiado a medir la Gran Pirámide de Keops en un solo día y sin la ayuda de instrumentos complejos. Ingenioso y gran observador como era, se le ocurrió una solución: si en algún momento del día su sombra tenía la misma longitud que él, entonces, en ese mismo instante, también la sombra de la pirámide sería igual a su altura y así sería posible medirla.
En teoría, la solución parecía fácil, pero llevarla a la práctica supondría un pequeño obstáculo: ¿cómo medir la propia sombra sin que ésta se moviera, perseguida por su propio eje como si fuera la traviesa sombra de Peter Pan? ¿Cómo saber el momento exacto en que tu sombra es igual a tu altura si cualquiera se da cuenta de que las sombras cambian con la hora del día?
Bueno, para Tales este obstáculo era «pan comido». Tendido sobre la arena marcó un círculo con un radio igual a su propia estatura y, de pie, se colocó en el centro a esperar a que los rayos de sol proyectaran la sombra ideal. Cuando ésta por fin tocó la circunferencia del círculo —y por ende, la longitud de la sombra era igual a su estatura— corrió a la Gran Pirámide para medir con una cuerda bien tensa la distancia existente entre la punta de la sombra y su base. Así, para sorpresa del pueblo egipcio, se conoció la altura exacta de la Gran Pirámide.
Pero Tales de Mileto no fue el único en aprovechar las sombras para fines científicos. Eratóstenes de Cirene (c a . 276-194 a.C.), gran geógrafo y tercer director de la Biblioteca de Alejandría —puesto que ocupó durante 41 años—, también lo haría para medir, nada más y nada menos, que la circunferencia de la Tierra.
Medirse con la Tierra
Aunque varios filósofos, escolásticos y navegantes europeos del siglo xv sabían que la Tierra era redonda —al contrario de la idea que se tiene del pensamiento medieval—, el misterio radicaba en desentrañar el tamaño real del planeta —Cristóbal Colón intentó convencer en vano a los cartógrafos de Isabel «La Católica» que las medidas de los griegos eran incorrectas— y en qué tan habitables serían otras latitudes. De ahí que no se aventuraran a explorar otros territorios, pues su temor no era producido por el «fin del mundo» que suponía una «Tierra plana», sino por mitos como el de la zona perusta de Aristóteles, quien consideraba que más allá del ecuador el ambiente era tan seco y caluroso que cualquier tripulación moriría calcinada por el ardor del sol.

Para entender el «sombrío» juego de Eratóstenes, es preciso remontarse a la antigua ciudad egipcia de Siena —hoy conocida como Asuán—, en el año 236 a.C. En cierto día del año, justo en el solsticio de verano, en esta localidad se daba un fenómeno peculiar: al mediodía, ni los obeliscos, ni las columnas, ni las varas clavadas sobre la tierra producían sombras. Eratóstenes se dio cuenta que el mismo día en que las sombras eran inexistentes en Siena, en Alejandría se mostraban largas y marcadas. De este modo llegó a una primera conclusión: si la Tierra fuera plana y considerando que el Sol estuviera lo suficientemente lejos para que sus rayos cayeran de forma paralela sobre el planeta, las sombras se proyectarían de la misma forma en todos lados. Pero como no sucedía así, pensó que entonces la Tierra debía ser redonda, y que entre más curva fuera cada zona, mayores serían las diferencias entre las sombras de un lugar a otro.
Obviamente, el sabio y culto «Pentatlón» —como le decían a Eratóstenes por practicar cinco disciplinas no precisamente olímpicas: poesía, matemáticas, filosofía, astronomía y geografía—, no se conformó con esa reflexión, y valiéndose de la observación y el razonamiento, formuló un experimento para medir la circunferencia de la Tierra: pensó que si el planeta era redondo como una naranja, bastaría con conocer uno de sus gajos para inferir su medida final, y para lograrlo, al igual que Tales de Mileto, sólo necesitaría de una sombra y una vara.
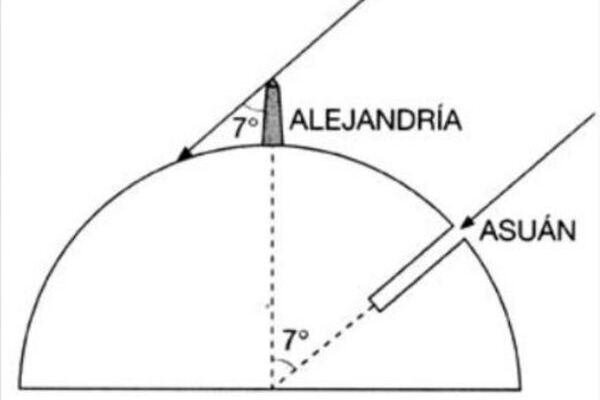
Imaginó una figura redonda y concluyó que el ángulo de la sombra proyectada por una vara en el patio de la Biblioteca de Alejandría, sería igual al ángulo formado por las verticales de las dos ciudades —Alejandría y Siena— si se prolongaran hasta el centro de la Tierra, como una rebanada al interior de un pastel.
Luego de realizar su experimento, midió el ángulo que se formaba entre su vara y la sombra, y gracias al Principio de los ángulos alternos internos infirió que si dicho ángulo era de 7.2º y un círculo tenía 360, entonces la parte extraída representaba una cincuentava parte de la Tierra.
Primero Alejandría, luego la Tierra
Ahora sólo faltaba conocer la distancia entre Alejandría y Siena. En aquella época, existían numerosos mapas del Nilo, pero ninguno mostraba distancias reales ni fiables para tal medición. Se dice que Eratóstenes recurrió entonces a las caravanas que iban de una a otra ciudad a lo largo del río Nilo: varios esclavos se encargaron de contar las vueltas que daban las ruedas de los carros, de contar pasos y recurrir a otros métodos de medición que existían en aquella época, para determinar la distancia entre las dos ciudades.
Nadie sabe cuántas personas participaron en hacer tal medición, pero sí que Eratóstenes estableció una medida promedio entre ambas ciudades de 5 000 estadios —que hoy serían unos 787.5 kilómetros—. Según su hipótesis, si el gajo entre Alejandría y Siena era una cincuentava parte del mundo, sólo habría que multiplicar 787.5 x 50 para obtener la circunferencia de la Tierra: 39 375 kilómetros. Hoy sabemos que la Tierra tiene una circunferencia de 40 000, lo que significa que Eratóstenes sólo tuvo 1.5% de error.
Pero este sorprendente cálculo estuvo a punto de desaparecer de los registros históricos por el funestamente célebre incendio de la Biblioteca de Alejandría, donde desapareció el equivalente a cien mil libros, entre los que se encontraba la Geografiká, obra de Eratóstenes de la que sólo se han encontrado algunos fragmentos dispersos. Es gracias al De Motu circulari corporum caelestium, del astrónomo griego Cleomedes —que apareció unos dos siglos después de la época de Eratóstenes—, que hoy podemos recordar esta hazaña.
Estas anécdotas comenzaron por seguir el paso de esas regiones de oscuridad, de esas siluetas negruscas que, a pesar de obstaculizar la luz, sirvieron como rayos de ingenio para encender las mentes que practicaron con maestría el arte tan fructífero de la observación.
Sigue leyendo:















