Desde las primeras ediciones de esta revista, uno de nuestros divulgadores de la ciencia favoritos ha sido el inigualable Isaac Asimov, cuya sencillez al explicar temas científicos complejos es una inspiración constante para quienes editamos Algarabía. En esta ocasión, el brillante científico nos lleva de la mano por la luna Es un artículo largo, así que pónganse cómodos.
❉
Casi todos los libros de astronomía que he leído, grandes o pequeños, contienen una breve tabla del Sistema Solar. Para cada planeta se da su diámetro, distancia al Sol, periodo de rotación, albedo, densidad, el número de sus lunas, y así sucesivamente.
Como estoy mórbidamente fascinado por los números, salto sobre dichas tablas con la perenne esperanza de encontrar nuevos elementos de información. Ocasionalmente soy recompensado con cosas tales como la temperatura de la superficie o la velocidad orbital, pero en realidad nunca obtengo lo suficiente.
De modo que de vez en cuando, cuando los circuitos de ingenuidad de mi cerebro emiten el rumor de que funcionan con razonable suavidad, deduzco nuevos tipos de datos para mí del material que tengo a la mano mientras pierdo el tiempo por algunas horas (al menos eso hacía en los ya lejanos días en los que podía perder el tiempo).
Todavía puedo hacerlo, siempre y cuando coloque los resultados en la estructura de un ensayo formal; así que vengan conmigo, divaguemos juntos de este modo y veamos qué pasa. Empecemos de esta manera, por ejemplo…
Consideraciones de gravedad

De acuerdo con Newton, cada objeto en el universo atrae a otro con una fuerza (f) que es proporcional al producto de sus masas (m1 y m2) dividido por el cuadrado de la distancia (d) entre ellos de centro a centro. Multiplicamos por la constante gravitacional (g) para convertir la proporcionalidad en igualdad, y tenemos:
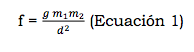
Esto significa, por ejemplo, que hay una atracción entre la Tierra y el Sol, y también entre la Tierra y la Luna, entre la Tierra y cada uno de los diferentes planetas, y, en este sentido, entre la Tierra y cualquier meteorito o pedazo de polvo cósmico en los cielos.
Afortunadamente, el Sol es abrumadoramente masivo comparado con todo lo demás en el Sistema Solar, de modo que al calcular la órbita de la Tierra o de cualquier otro planeta, una excelente primera aproximación se obtiene si únicamente son considerados el planeta y el Sol, como si estuvieran solos en el universo. El efecto de otros cuerpos puede ser calculado después para refinamientos relativamente menores.
Del mismo modo, la órbita de un satélite puede ser calculada suponiendo primero que está solo en el universo con su planeta primario.
Es en este punto que algo me interesa. Si el Sol es mucho más masivo que cualquier planeta, ¿no debería ejercer una atracción considerable sobre el satélite aunque esté a una distancia mucho mayor que a la que está el planeta primario? Si es así, ¿qué tan considerable es «considerable»?
Jalando la cuerda
Para ponerlo de otro modo, supongan que visualizamos un juego de jalar a la cuerda llevándose a cabo para cada satélite, con su primario de un lado de la cuerda gravitacional y el Sol del otro. En este juego de jalar a la cuerda, ¿qué tan bien le está yendo al Sol?
Supongo que los astrónomos han calculado estas cosas, pero nunca he visto los resultados reportados en ningún texto de astronomía, o siquiera el tema discutido, de modo que lo haré yo.
Aquí está cómo podemos abordarlo. Llamemos «m» a la masa de un satélite, «mp» a la masa de su planeta primario (con lo que, por cierto, me refiero al planeta que circunda) y «ms» a la del Sol. La distancia del satélite a su primario será «dp» y la distancia del satélite al Sol, «ds». La fuerza gravitacional entre el satélite y su primario sería «fp», y aquélla entre el satélite y el Sol, «fs», y eso es todo. Prometo no usar otros símbolos en este capítulo.
De la ecuación 1 podemos decir que la fuerza de atracción entre un satélite y su planeta primario sería:
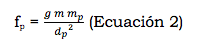
mientras que entre el mismo satélite y el Sol, sería:
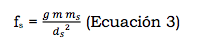
En lo que estamos interesados es en saber cómo es la fuerza gravitacional entre el satélite y su planeta primario comparada con aquélla entre el satélite y el Sol. En otras palabras, queremos la razón fp/fs, a la cual podemos llamar el «valor del juego de jalar a la cuerda».
Para obtenerlo debemos dividir la ecuación 2 entre la ecuación 3. El resultado de dicha división sería: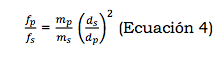
Al hacer la división, varias simplificaciones han tenido lugar. Por un lado, la constante gravitacional se ha eliminado, lo cual significa que no tendremos que molestarnos con un número inconvenientemente pequeño ni con algunas unidades igualmente inconvenientes. Por otro lado, la masa del satélite se ha cancelado. (En otras palabras, al obtener el valor del juego de jalar a la cuerda no importa qué tan grande o pequeño sea un satélite en particular. El resultado sería el mismo en cualquier caso.)
Lo que necesitamos para el valor del juego de jalar a la cuerda fp/fs es la razón de la masa del planeta a la del Sol mp/ms y el cuadrado de la razón de la distancia del planeta al Sol a la del satélite a su planeta primario: ds/dp2.
Satélites y planetas
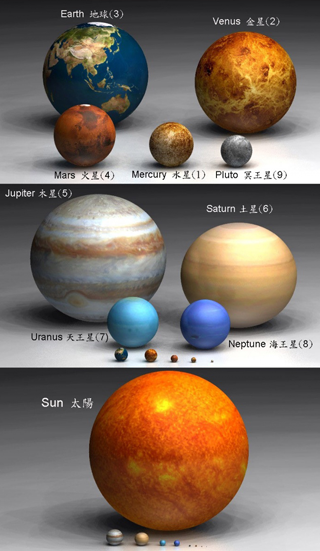
Hay solamente seis planetas que tienen satélites, y estos, en orden decreciente de acuerdo a su distancia al Sol, son: Neptuno, Urano, Saturno, Júpiter, Marte y la Tierra. (Coloco a la Tierra al final en lugar de al principio, como dictaría el chauvinismo natural, por mis propias razones. Ya verán.)
Para éstos, calcularemos primero la razón de las masas y los resultados quedan como sigue:
| Neptuno | 0.000052 |
| Urano | 0.000044 |
| Saturno | 0.00028 |
| Júpiter | 0.00095 |
| Marte | 0.00000033 |
| Tierra | 0.0000030 [sic] |
Como se puede apreciar, la razón de las masas está ampliamente a favor del Sol. Incluso Júpiter, que es por mucho el más masivo de los planetas, no tiene siquiera la milésima parte de la masa del Sol. De hecho, todos los planetas juntos (mas los satélites, planetoides, cometas y meteoros) no conforman más de 1/750 de la masa del Sol.
Hasta ahora, entonces, el juego de jalar a la cuerda está completamente cargado hacia el lado del Sol. Sin embargo, debemos a continuación obtener las razones de las distancias, y eso favorece enormemente al planeta, porque cada satélite está, por supuesto, muchísimo más cercano a su planeta primario que al Sol. Y lo que es más, esta razón favorable (para el planeta) debe elevarse al cuadrado, haciéndola más favorable aún, así que al final podemos estar razonablemente seguros de que el Sol terminará perdiendo en el juego de jalar a la cuerda. Pero verificaremos de cualquier modo.
Neptuno

Tomemos Neptuno en primer lugar. Tiene dos satélites: Tritón y Nereida. La distancia promedio de cada uno de ellos al Sol es, de modo necesario, precisamente la misma que la distancia promedio de Neptuno al Sol, que es de 2,797,000,000 millas. La distancia promedio de Tritón a Neptuno es, sin embargo, de solamente 220,000 millas, mientras que la distancia promedio de Nereida a Neptuno es de 3,460,000 millas.
Si dividimos la distancia al Sol entre la distancia a Neptuno para cada satélite y elevamos al cuadrado el resultado, obtenemos 162,000,000 para Tritón y 655,000 para Nereida. Multiplicamos cada una de estas cantidades por la razón de las masas entre Neptuno y el Sol, y eso nos da el valor del juego de jalar a la cuerda, que es:
| Tritón | 8,400 |
| Nereida | 34 |
Las condiciones difieren marcadamente para los dos satélites. La influencia gravitacional de Neptuno sobre su satélite más cercano, Tritón, es abrumadoramente mayor que la del Sol sobre el mismo satélite. Tritón está bien agarrado de Neptuno. El satélite exterior, Nereida, sin embargo, es atraído considerablemente por Neptuno, pero no abrumadoramente más que por el Sol. De forma adicional, Nereida tiene una órbita altamente excéntrica, la más excéntrica de las de cualquier satélite del sistema. Se aproxima a 800,000 millas de Neptuno en un extremo de su órbita y retrocede tan lejos como 6 millones de millas en el otro. Cuando está más distante de Neptuno, ¡Nereida experimenta un valor del juego de jalar a la cuerda tan pequeño como once!
Por una variedad de razones (la excentricidad de la órbita de Nereida entre ellas) por lo general los astrónomos suponen que Nereida no es un satélite verdadero de Neptuno, sino un planetoide capturado por él en la ocasión de una aproximación demasiado cercana.
El débil agarre de Neptuno sobre Nereida ciertamente parece apoyar esto. De hecho, desde el punto de vista amplio de la astronomía, la asociación entre Neptuno y Nereida puede ser temporal. Tal vez el efecto perturbador del jalón solar finalmente lo quitará de la sujeción de Neptuno. Tritón, por otro lado, nunca dejará la compañía de Neptuno a no ser por alguna catástrofe a escala del sistema.
Urano

No hay necesidad de detallar los cálculos para todos los satélites. Haré el trabajo y les entregaré los resultados. Urano, por ejemplo, tiene cinco satélites conocidos, todos dando vueltas en el plano de su ecuador y todos considerados satélites verdaderos por los astrónomos.
Haciendo el recorrido hacia afuera desde el planeta, son: Miranda, Ariel, Umbriel, Titania y Oberón. Los valores del juego de jalar a la cuerda para estos satélites son:
| Miranda | 24,600 |
| Ariel | 9,850 |
| Umbriel | 4,750 |
| Titania | 1,750 |
| Oberón | 1,050 |
Todos están segura y abrumadoramente en el agarre de Urano, y los altos valores del juego de jalar a la cuerda coinciden con su estatus de satélites verdaderos.
Saturno

Pasamos entonces a Saturno, que tiene nueve satélites: Mimas, Encélado, Tetis, Dione, Rea, Titán, Hiperión, Jápeto y Febe. De estos, los ocho más cercanos al planeta dan vueltas en el plano de su ecuador y son considerados satélites verdaderos. Febe, el noveno, posee una órbita altamente inclinada y es considerado un planetoide capturado.
Los valores del juego de jalar a la cuerda para estos satélites son:
| Mimas | 15,500 |
| Encélado | 9,800 |
| Tetis | 6,400 |
| Dione | 4,150 |
| Rea | 2,000 |
| Titán | 380 |
| Hiperión | 260 |
| Jápeto | 45 |
| Febe | 31 |
Nótese el bajo valor para Febe.
Júpiter

Júpiter tiene doce satélites y los tomaré en dos instancias. Los primeros cinco: Amaltea, Io, Europa, Ganímedes y Calisto dan vueltas en el plano del ecuador de Júpiter y todos se consideran satélites verdaderos. Los valores del juego de jalar a la cuerda para ellos son:
| Amaltea | 18,200 |
| Io | 3,260 |
| Europa | 1,260 |
| Ganímedes | 490 |
| Calisto | 160 |
y todos están claramente en el agarre de Júpiter.
Júpiter, sin embargo, tiene otros siete satélites, los cuales no tienen nombre oficial, y son comúnmente conocidos por numerales romanos (del VI al XII) dados en el orden de su descubrimiento. En el orden de la distancia desde Júpiter son VI, X, VII, XII, XI, VIII y IX.
Todos son pequeños y con órbitas excéntricas y altamente inclinadas respecto al plano del ecuador de Júpiter. Los astrónomos los consideran planetoides capturados (Júpiter es mucho más masivo que los otros planetas y está más cerca del cinturón de asteroides, así que no es sorprendente que capturara siete planetoides).
Los resultados del juego de jalar a la cuerda para estos siete ciertamente soportan la noción de que son planetoides capturados, porque los valores son:
| VI | 4.4 |
| X | 4.3 |
| VII | 4.2 |
| XII | 1.3 |
| XI | 1.2 |
| VIII | 1.03 |
| IX | 1.03 |
El agarre de Júpiter sobre estos satélites exteriores es débil en verdad.
Marte

Marte tiene dos satélites, Fobos y Deimos, pequeños y muy cercanos a Marte. Rotan en el plano del ecuador de Marte, y son considerados satélites verdaderos. Los valores del juego de jalar a la cuerda son:
| Fobos | 195 |
| Deimos | 32 |
Planetas exteriores
Hasta ahora he enlistado 30 satélites, de los cuales 21 son considerados verdaderos, y nueve son usualmente clasificados como (probables) planetoides capturados. Me gustaría por el momento, dejar fuera de consideración el trigésimo primer satélite, que sucede que es nuestra propia Luna (regresaré a ella, lo prometo), y resumir los 30 como sigue:
| Número de satélites |
| Planeta | Verdadero | Capturado |
| Neptuno | 1 | 1 |
| Urano | 5 | 0 |
| Saturno | 8 | 1 |
| Júpiter | 5 | 7 |
| Marte | 2 | 0 |
Es poco probable que algún satélite verdadero adicional sea descubierto (aunque, ciertamente, Miranda fue descubierto tan recientemente como 1948). Sin embargo, una cantidad de cuerpos bajo la clasificación de planetoides capturados pueden todavía surgir, particularmente una vez que efectivamente salgamos y veamos. Pero ahora analicemos esta lista en términos de los valores del juego de jalar a la cuerda. Entre los satélites verdaderos, el valor más bajo es el de Deimos, 32. Por otro lado, entre los nueve satélites listados como planetoides capturados, el valor más alto es el de Nereida con un promedio de 34.
Aceptemos este estado de las cosas y asumamos que el valor del juego de jalar a la cuerda de 30 es un mínimo razonable para un satélite verdadero y que cualquier satélite con un valor menor es, con toda probabilidad, capturado y probablemente un miembro temporal de la familia del planeta.
Al conocer la masa de un planeta y su distancia al Sol podemos calcular la distancia desde el centro del planeta a la cual este valor del juego de jalar a la cuerda se encontrará. Podemos usar la ecuación 4 para tal propósito, haciendo fp/fs igual a 30, poniendo los valores conocidos para las masas y la distancia «ds», y resolviendo para «dp». Ésa será la máxima distancia a la cual podemos esperar encontrar un satélite verdadero. El único planeta que no puede ser manipulado de este modo es Plutón, cuyo valor de masa es muy incierto, por lo que omito a Plutón alegremente.
También podemos establecer una distancia mínima a la cual podemos esperar un satélite verdadero; o, por lo menos, un satélite verdadero de la forma usual. Ha sido calculado que si un satélite verdadero está más cerca a su primario que cierta distancia, las fuerzas de marea lo romperán en pedazos. A la inversa, si ya existen fragmentos a dicha distancia, no se consolidarán en un solo cuerpo. Este límite de distancia es conocido como el “límite Roche”, así nombrado por el astrónomo E. Roche, quien lo calculó en 1849. El límite Roche es una distancia desde un centro planetario igual a 2.44 veces el radio del planeta.
Así, ahorrándoles los cálculos, aquí están los resultados para los cuatro planetas exteriores:
| Distancia del satélite verdadero (millas desde el centro primario) |
| Planeta | Máximo (valor del juego de jalar la cuerda=30) |
Mínimo (límite Roche) |
| Neptuno | 3,700,000 | 38,000 |
| Urano | 2,200,000 | 39,000 |
| Saturno | 2,700,000 | 87,000 |
| Júpiter | 2,700,000 | 106,000 |
Como pueden ver, cada uno de estos planetas exteriores, con grandes masas y lejos de la competencia del Sol, tiene amplio espacio para grandes y complejos sistemas satelitales en estos límites generosos, y los 21 satélites verdaderos todos caen dentro de esos límites.
Saturno sí posee algo dentro del límite Roche: su sistema de anillos. La orilla exterior del sistema de anillos se extiende a 85,000 millas del centro del planeta. Obviamente el material en los anillos podría haber sido recolectado en un satélite verdadero si no hubiera estado tan cerca a Saturno.
El sistema de anillos es único en lo que concierne a los planetas visibles, pero por supuesto que los únicos planetas que podemos ver son los de nuestro propio Sistema Solar. Aún entre estos, los únicos que podemos considerar razonablemente en conexión con satélites (explicaré el porqué en un momento) son los cuatro grandes.
De estos, Saturno tiene un sistema de anillos y Júpiter por nada tiene uno. Su satélite más interno, Amaltea, está a aproximadamente 110,000 millas del centro del planeta, con el límite Roche a 106,000 millas. Unas pocas millas más adentro y Júpiter tendría anillos.
Me gustaría hacer la sugerencia entonces de que una vez que salgamos a explorar otros sistemas estelares descubriremos (probablemente para nuestro asombro inicial) que cerca de la mitad de los grandes planetas que encontremos estarán equipados con anillos al modo de Saturno.
A continuación podemos intentar hacer lo mismo con los planetas interiores. Como ellos son, todos, mucho menos masivos que los exteriores, y mucho más cercanos a la competencia del Sol, podríamos anticipar que el rango de distancias abiertas a la formación de satélites verdaderos estaría más restringido, y estaríamos en lo correcto. Aquí están las cantidades como las calculé:
| Distancia del satélite verdadero (millas desde el centro primario) |
| Planeta | Máximo (valor del juego de jalar la cuerda=30) |
Mínimo (límite Roche) |
| Marte | 15,000 | 5,150 |
| Tierra | 29,000 | 9,600 |
| Venus | 19,000 | 9,200 |
| Mercurio | 1,300 | 3,800 |
Planetas interiores
Así, como ven, mientras que cada planeta exterior tiene un rango de dos millones de millas o más en el que podrían formarse satélites verdaderos, la situación es mucho más restringida para los planetas interiores. Marte y Venus tienen un rango permisible de alrededor de 10,000 millas. A la Tierra le va un poco mejor con 20,000 millas.
Mercurio es el caso más interesante. La distancia máxima a la que puede esperarse que se forme un satélite natural contra la abrumadora competencia del cercano Sol está claramente dentro del límite Roche. De ello se sigue, si mi razonamiento es correcto, que Mercurio no puede tener un satélite verdadero, y que nada diferente a un posible esparcimiento de grava puede esperarse.
En realidad, ningún satélite ha sido localizado para Mercurio, pero, hasta donde yo sé, nadie se ha ocupado en presentar una razón para esto o tratarlo como algo más que un dato empírico. Si algún lector gentil con algún conocimiento mayor de detalles astronómicos que el mío propio me escribiera para decirme que he sido anticipado en esto, y por quién, trataré de tomar la noticia filosóficamente. Por lo menos confinaré mi berrinche a la privacidad de mi estudio.
Venus, la Tierra y Marte están mejor que Mercurio y tienen un poco de espacio para satélites verdaderos más allá del límite Roche. No es mucho, sin embargo, y las oportunidades de juntar material suficiente en tan pequeño volumen de espacio para hacer aunque sea un satélite pequeñito son menudas.
Y sucede que ni Venus ni la Tierra tienen ningún satélite (excepto por posibles pedazos menudos de grava) dentro de los límites indicados, y Marte tiene dos pequeños satélites, uno de tal vez 12 millas de diámetro y el otro de 6, que escasamente merecen el nombre.
La Luna

Es sorprendente, y muy gratificante para mí, notar cómo todo tiene deliciosamente sentido y qué bien puedo razonar los detalles de los sistemas de satélites de los diversos planetas. Es una pena que una cosita permanezca sin ser tenida en cuenta, una insignificancia que he ignorado hasta ahora, pero ¿QUÉ DIANTRES HACE NUESTRA LUNA TAN LEJOS? Está demasiado lejos para ser un satélite verdadero de la Tierra, si seguimos por mi bella cadena de razonamiento, la cual es demasiado bella para mí como para abandonarla. Es demasiado grande como para haber sido capturada por la Tierra. La probabilidad de que tal captura haya tenido efecto y que la Luna después haya tomado una órbita casi circular alrededor de la Tierra es muy pequeña para que tal eventualidad sea creíble.
Hay teorías, por supuesto, al efecto de que la Luna estuvo alguna vez mucho más cercana a la Tierra (dentro de mis límites permitidos para un satélite verdadero) y entonces se movió gradualmente hacia afuera como resultado de la acción de la marea. Bien, tengo una objeción a eso: si la Luna fuera un satélite verdadero que originalmente hubiera rondado a la Tierra a una distancia de, digamos, 20,000 millas, estaría casi con seguridad orbitando en el plano del ecuador terrestre, y no es así.
Pero, entonces, si la Luna no es un satélite verdadero de la Tierra ni uno capturado, ¿qué es? Esto puede sorprenderlos, pero tengo una respuesta; y para explicarla, regresemos a mis determinaciones del juego de jalar a la cuerda. Hay, después de todo, un satélite para el cual no lo he calculado, y ése es nuestra propia Luna. Lo haremos ahora.
La distancia promedio de la Luna a la Tierra es de 237,000 millas, y la distancia promedio de la Luna al Sol es de 93,000,000 de millas. La razón de la distancia Luna-Sol a la distancia Luna-Tierra es 392. Elevando al cuadrado nos da 154,000 (sic). La razón de la masa de la Tierra a la del Sol fue dada más arriba y es de 0.0000030 (sic).
Multiplicando esta cantidad por 154,000 nos da el valor del juego de jalar a la cuerda, lo que resulta en:
| Luna | 0.46 |
La Luna, en otras palabras, es única entre los satélites del Sistema Solar en el sentido de que su primario (nosotros) pierde el juego de jalar a la cuerda con el Sol. El Sol atrae a la Luna dos veces más fuertemente que la Tierra.
Podríamos ver a la Luna, entonces, no como un satélite verdadero de la Tierra ni como uno capturado, sino como un planeta por derecho propio, moviéndose alrededor del Sol en una caminata cuidadosa con la Tierra. Ciertamente, desde el punto de vista del sistema Tierra-Luna, la manera más simple de imaginarse la situación es tener a la Luna girando alrededor de la Tierra; pero si tuvieran qué hacer un dibujo de las órbitas de la Tierra y la Luna alrededor del Sol exactamente a escala, verían que la órbita de la Luna es en todos lados cóncava hacia el Sol. Está siempre “cayendo” hacia el Sol. Todos los demás satélites, sin excepción, “caen” alejándose del Sol en parte de sus órbitas, atrapados como están por el jalón superior de su primario, pero no la Luna.
Y consideren esto: la Luna no gira alrededor de la Tierra en el plano del ecuador terrestre, como se esperaría de un satélite verdadero. Más bien gira alrededor de la Tierra en un plano muy cercano al de la eclíptica, esto es, el plano en el que los planetas generalmente rotan alrededor del Sol. ¡Esto es justo lo que se esperaría de un planeta!
¿Es posible entonces que haya un punto intermedio entre la situación de un planeta masivo distante del Sol, el cual se desarrolla a partir de un solo núcleo, con numerosos satélites formados, y la de un planeta pequeño cercano al Sol desarrollado a partir de un solo núcleo sin satélites? ¿Puede haber una condición frontera, por decirlo así, en el que haya una condensación a partir de dos núcleos de modo que se forme un planeta doble?
Tal vez la Tierra atinó apenas la orilla de la masa y la distancia permisibles; un poco demasiado pequeña, un poco demasiado cerca.
Quizá si hubiera estado mejor situada, las dos mitades del planeta doble hubieran sido un poco más parecidas en tamaño. Quizá las dos hubieran tenido atmósferas y océanos y vida. Quizá en otros sistemas estelares con un planeta doble, una mayor igualdad es más usual.
¡Qué pena que nos hayamos perdido eso!
O tal vez (quién sabe), ¡qué suerte!
❉❉❉
Sigue leyendo en Algarabía
Los nombres de las lunas llenas
¿Qué es una miniluna?
El mayor sueño de la Humanidad: de la Tierra a la Luna















