La palabra dimensión viene del término latino dimensio que significa «medir completamente». Vayamos, pues, con algunas medidas.
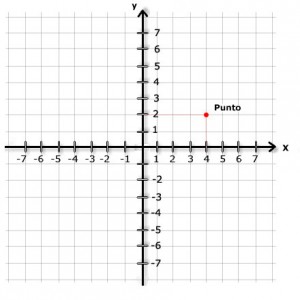
Supongamos que tiene una línea recta y que quiere marcar sobre ella un punto fijo x, de manera que cualquier otra persona pueda encontrarlo con sólo leer su descripción. Para empezar, hace una señal en cualquier lugar de la línea y la llama cero, mide luego y comprueba que x está exactamente a dos pulgadas de la marca del cero. Si está a uno de los lados, conviene en llamar a esa distancia +2; si está al otro, -2. El punto queda así localizado con un solo número, siempre que los demás acepten esas «convenciones»: la marca del cero, el lado que es más y el lado que es menos.
Como para localizar un punto sobre una línea sólo se necesita un número, la línea o cualquier trozo de ella es unidimensional: un solo número mide completamente. Pero supongamos que tiene una gran hoja de papel y que quiere localizar en ella un punto fijo x. Empieza en la marca del cero y comprueba que está a cinco pulgadas… pero, ¿en qué dirección? Lo que puede hacer es descomponer la distancia en dos direcciones. Tres pulgadas al norte y cuatro al este. Si llamamos al norte más, al sur menos, al este más y al oeste menos, podrá localizar el punto con dos números: +3, +4.
O también puede decir que está a cinco pulgadas del cero en un ángulo de 36.87º de la línea este-oeste. De nuevo dos números: 5 y 36.87° . Haga lo que haga, siempre necesitará dos números para localizar un punto fijo en el interior de un plano; el plano es, por tanto, bidimensional.
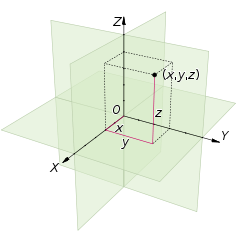
Supongamos ahora que lo que tenemos es un punto fijo dentro de un espacio, como en una habitación. Éste se podrá localizar diciendo que está, por ejemplo, a cinco pulgadas al norte de la marca cero, tres pulgadas al este y siete pulgadas encima de ésta. O simplemente dando una distancia y dos ángulos. De esta forma siempre se necesitarán tres números para localizar un punto dentro de una habitación o dentro del Universo, por lo tanto éstos son tridimensionales.
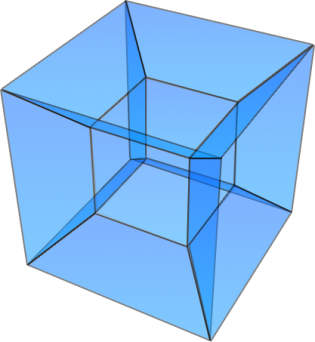
Supongamos que hubiese un espacio de naturaleza tal que se necesitaran cuatro números, o cinco, o 18, para localizar un punto fijo en él. Sería un espacio cuadridimensional, o de cinco dimensiones, o de 18 dimensiones. Tales espacios no existen en el universo ordinario, pero en matemáticas sí se pueden concebir estos «hiperespacios» y calcular
qué propiedades tendrían las correspondientes figuras matemáticas.
Incluso, se pueden calcular las propiedades que se cumplirían para cualquier espacio dimensional, lo que se llama «geometría n-dimensional».
Pero, ¿y si lo que estamos usando son puntos variables en el tiempo, es decir, que no están fijos? Por ejemplo, si queremos localizar la posición de un mosquito que está volando en
una habitación, tendremos que dar los tres números que ya conocemos: norte-sur, este-oeste y arriba-abajo. Pero luego tendríamos que añadir un cuarto número que representara el tiempo, porque el mosquito sólo habrá ocupado esa posición especial durante un instante y hay que identificarlo.
Lo mismo vale para todo cuanto hay en el Universo. Tenemos el espacio, que es tridimensional, y hay que añadir el tiempo para obtener un «espacio-tiempo» tetradimensional, pero dándole un tratamiento diferente al de las tres «dimensiones espaciales». En ciertas ecuaciones clave en las que los símbolos de las tres dimensiones especiales tienen signo positivo, el símbolo del tiempo es negativo.
Por tanto, no debemos decir que el tiempo es «la cuarta» dimensión. Es sólo «una» cuarta dimensión, diferente de las otras tres. [Este texto fue publicado por primera vez en 1973. Actualmente, los investigadores discuten si existe una cuarta dimensión espacial, es decir, una cuarta dimensión ortogonal o perpendicular a las tres dimensiones que conocemos. Si consideramos que el tiempo es la cuarta dimensión, entonces podríamos decir que esta hipotética cuarta dimensión espacial es en realidad la quinta dimensión.]















